Sem II IT Structure of Tree
There are many basic data structures that can be used to solve application problems. Array is a good static data structure that can be accessed randomly and is fairly easy to implement. Linked Lists on the other hand is dynamic and is ideal for application that requires frequent operations such as add, delete, and update. One drawback of linked list is that data access is sequential. Then there are other specialized data structures like, stacks and queues that allows us to solve complicated problems (eg: Maze traversal) using these restricted data structures. One other data structure is the hash table that allows users to program applications that require frequent search and updates. They can be done in O(1) in a hash table.
One of the disadvantages of using an array or linked list to store data is the time necessary to search for an item. Since both the arrays and Linked Lists are linear structures the time required to search a “linear” list is proportional to the size of the data set. For example, if the size of the data set is n, then the number of comparisons needed to find (or not find) an item may be as bad as some multiple of n. So imagine doing the search on a linked list (or array) with n = 106 nodes. Even on a machine that can do million comparisons per second, searching for m items will take roughly m seconds. This not acceptable in today’s world where speed at which we complete operations is extremely important. Time is money. Therefore it seems that better (more efficient) data structures are needed to store and search data.
A tree is a nonlinear hierarchical data structure that consists of nodes connected by edges.
A Tree
Why Tree Data Structure?
Other data structures such as arrays, linked list, stack, and queue are linear data structures that store data sequentially. In order to perform any operation in a linear data structure, the time complexity increases with the increase in the data size. But, it is not acceptable in today's computational world.
Different tree data structures allow quicker and easier access to the data as it is a non-linear data structure.
Tree Terminologies
Node
A node is an entity that contains a key or value and pointers to its child nodes.
The last nodes of each path are called leaf nodes or external nodes that do not contain a link/pointer to child nodes.
The node having at least a child node is called an internal node.
Edge
It is the link between any two nodes.
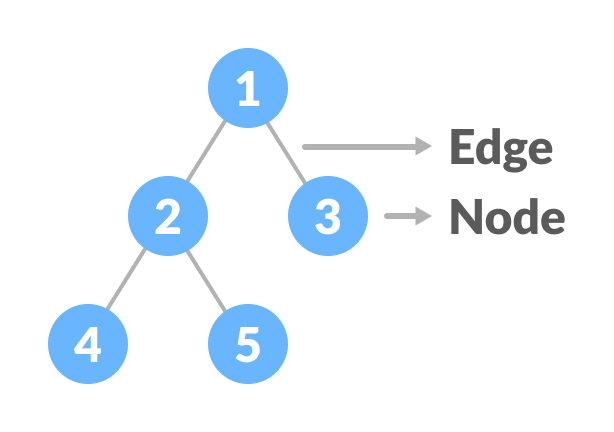Nodes and edges of a tree
Root
It is the topmost node of a tree.
Height of a Node
The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).
Depth of a Node
he depth of a node is the number of edges from the root to the node.
Height of a Tree
The height of a Tree is the height of the root node or the depth of the deepest node.
Height and depth of each node in a tree
Degree of a Node
The degree of a node is the total number of branches of that node.
ypes of Tree
-
Binary Tree
-
Binary Search Tree
-
AVL Tree
-
B-Tree
Tree Traversal
In order to perform any operation on a tree, you need to reach to the specific node. The tree traversal algorithm helps in visiting a required node in the tree.
To learn more, please visit tree traversal.
Tree Applications
-
Binary Search Trees(BSTs) are used to quickly check whether an element is present in a set or not.
-
Heap is a kind of tree that is used for heap sort.
-
A modified version of a tree called Tries is used in modern routers to store routing information.
-
Most popular databases use B-Trees and T-Trees, which are variants of the tree structure we learned above to store their data
-
Compilers use a syntax tree to validate the syntax of every program you write.